Sai số chuẩn độ (Standard Error) là một khái niệm thống kê quan trọng để đo lường độ biến động và sự không chắc chắn trong dữ liệu. Nó đóng vai trò quan trọng trong việc xác định độ chính xác của ước lượng thống kê và dự đoán. Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm, cách tính Sai số chuẩn độ và ý nghĩa trong nghiên cứu và thống kê.
1. Sai số chuẩn độ là gì?
Sai số chuẩn độ (standard deviation) là một đại lượng thống kê dùng để đo sự biến đổi, phân tán của dữ liệu trong một tập hợp. Nó cho biết mức độ mà các giá trị trong tập hợp dữ liệu gần hay xa so với giá trị trung bình của tập hợp đó.
Sai số chuẩn độ thường được ký hiệu là σ (sigma) trong thống kê.
2. Công thức tính Sai số chuẩn độ
Công thức tính sai số chuẩn độ của một tập hợp dữ liệu là:
σ = √Σ(xi – μ)² / N
Trong đó:
σ là sai số chuẩn độ.
xi là từng giá trị trong tập dữ liệu.
μ là giá trị trung bình của tập dữ liệu.
N là số lượng giá trị trong tập dữ liệu.
Sai số chuẩn độ cho biết mức độ biến đổi của dữ liệu. Nếu sai số chuẩn độ lớn, tức là giá trị của các điểm dữ liệu trong tập hợp có sự biến đổi lớn so với giá trị trung bình. Ngược lại, nếu sai số chuẩn độ nhỏ, thì dữ liệu có xu hướng tập trung xung quanh giá trị trung bình.
Sai số chuẩn độ thường được sử dụng để đánh giá độ tin cậy của dữ liệu, đo lường sai lệch trong dự đoán và phân tích phân phối của dữ liệu trong nhiều lĩnh vực, bao gồm thống kê, khoa học dữ liệu, kế toán, và nhiều ứng dụng khác.
3. Ví dụ về Sai số chuẩn độ
Dưới đây là một ví dụ về việc sử dụng sai số chuẩn độ để đo độ biến đổi trong dữ liệu:
Ví dụ:
Giả sử bạn đang làm việc trong một công ty sản xuất điện thoại di động và bạn muốn đo độ biến đổi trong thời gian cần để sản xuất một chiếc điện thoại. Bạn đã thu thập dữ liệu về thời gian sản xuất (tính bằng giờ) cho 100 chiếc điện thoại và muốn biết xem liệu quy trình sản xuất có ổn định hay không.
Dữ liệu về thời gian sản xuất 100 chiếc điện thoại như sau:
1 giờ, 2 giờ, 3 giờ, 2 giờ, 1.5 giờ, 2.5 giờ, 2.2 giờ, 3 giờ, 2.7 giờ, 2 giờ, …
Đầu tiên, bạn tính giá trị trung bình của thời gian sản xuất (μ):
μ = (1 + 2 + 3 + 2 + 1.5 + 2.5 + 2.2 + 3 + 2.7 + 2 + …) / 100
Sau đó, bạn tính sai số chuẩn độ (σ) bằng cách sử dụng công thức:
σ = √Σ(xi – μ)² / N
Trong trường hợp này, bạn tính toán sự biến đổi của thời gian sản xuất so với giá trị trung bình và sau đó tính sai số chuẩn độ. Nếu σ lớn, thì quy trình sản xuất không ổn định, và thời gian sản xuất thay đổi nhiều. Nếu σ nhỏ, thì quy trình sản xuất ổn định hơn và thời gian sản xuất gần giá trị trung bình.
Sai số chuẩn độ sẽ giúp bạn đánh giá mức độ biến đổi trong thời gian sản xuất và đưa ra quyết định về việc cải thiện quy trình sản xuất để làm cho nó ổn định hơn nếu cần thiết.
4. Cách tính Sai số chuẩn độ bằng SPSS
Để tính sai số chuẩn độ (standard error) trong SPSS, bạn cần thực hiện một phân tích thống kê dựa trên dữ liệu mà bạn có. Sai số chuẩn độ thường được sử dụng để đo mức độ biến động của dữ liệu quan sát so với giá trị trung bình. Dưới đây là cách tính sai số chuẩn độ bằng SPSS:
Mở dữ liệu và chuẩn bị dữ liệu của bạn:
- Mở SPSS và mở tập tin dữ liệu mà bạn muốn thực hiện phân tích trên.
- Đảm bảo dữ liệu của bạn đã được nhập và biến cần tính sai số chuẩn độ đã được xác định.
Chọn thống kê cơ bản:
- Chọn “Analyze” (phân tích) từ thanh công cụ trên cùng.
- Chọn “Descriptive Statistics” (thống kê mô tả) từ menu con.
Cấu hình cửa sổ “Descriptives”:
- Trong cửa sổ “Descriptives,” chọn biến mà bạn muốn tính sai số chuẩn độ.
- Chọn “Standard error” trong phần “Options.”
Nhấn nút “OK” để tính toán sai số chuẩn độ.
- Khi bạn nhấn nút “OK,” SPSS sẽ tính sai số chuẩn độ cho biến bạn đã chọn và hiển thị nó trong bảng kết quả.
Nếu bạn đang gặp khó khăn hoặc cần sự hỗ trợ, đừng ngần ngại hãy liên hệ với dịch vụ chạy SPSS thuê của Luận Văn Việt. Chúng tôi cam kết cung cấp dịch vụ uy tín và chất lượng hàng đầu tại Việt Nam, với mức giá hợp lý và bảo mật thông tin khách hàng được đặt lên hàng đầu. Hãy để chúng tôi giúp bạn!
5. Ví dụ cách tính sai số chuẩn độ bằng SPSS
Ví dụ: Bạn đang nghiên cứu về chiều cao của học sinh trong một lớp học. Bạn đã thu thập dữ liệu về chiều cao của 30 học sinh và muốn tính Sai số chuẩn độ cho biến chiều cao của họ.
Dưới đây là cách bạn có thể tính Sai số chuẩn độ cho biến chiều cao trong SPSS:
Bước 1: Mở dự án SPSS và nhập dữ liệu
Mở SPSS và tạo một tài liệu dự án mới.
Nhập dữ liệu về chiều cao của 30 học sinh vào tài liệu dự án.
Bước 2: Chọn “Analyze” và “Descriptive Statistics”
Chọn tab “Analyze” từ thanh công cụ trên cùng.
Chọn “Descriptive Statistics” trong menu con.
Bước 3: Cấu hình cửa sổ “Descriptives”
Trong cửa sổ “Descriptives,” di chuyển biến “Chiều cao” từ cửa sổ “Variables” sang ô “Dependent List.”
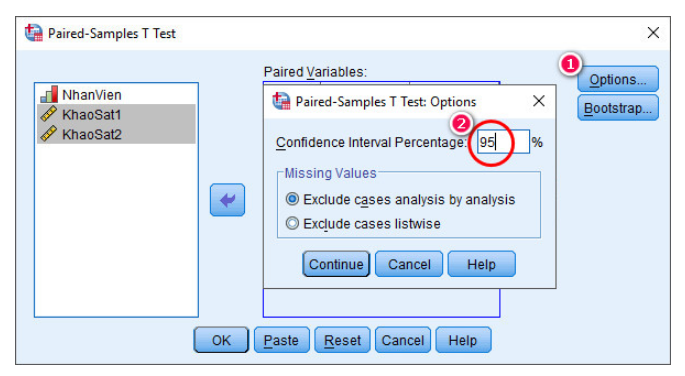
Bước 4: Chọn “Options” để tính Sai số chuẩn độ
Khi bạn đã chọn biến chiều cao, nhấn vào nút “Options” ở phía dưới.
Bước 5: Trong cửa sổ “Descriptives: Options”, đảm bảo rằng bạn đã chọn “Standard error” trong danh sách các phép tính.
Bước 6: Nhấn “Continue” và sau đó “OK” để tính toán Sai số chuẩn độ
Khi bạn nhấn “OK”, SPSS sẽ thực hiện tính toán và hiển thị kết quả trong bảng kết quả. Trong bảng này, bạn sẽ thấy Sai số chuẩn độ (Standard Error) cho biến chiều cao của các học sinh.
4. So sánh Sai số chuẩn độ và Sai số chuẩn
| Đặc Điểm | Sai Số Chuẩn (Standard Deviation) | Sai Số Chuẩn Độ (Standard Error) |
| Mục tiêu | Đo độ biến đổi của dữ liệu trong một tập hợp dữ liệu. | Đo độ biến đổi của mẫu ngẫu nhiên từ một tập dữ liệu lớn. |
| Ký hiệu | σ (sigma) | SE hoặc SEM |
| Ứng dụng | Đánh giá độ biến đổi của dữ liệu và phân phối dữ liệu. | Sử dụng để ước tính mức độ không chắc chắn trong việc suy ra từ một mẫu ngẫu nhiên đến quần thể. |
| Liên quan đến | Dữ liệu gốc | Mẫu ngẫu nhiên từ dữ liệu gốc để ước tính thông tin về quần thể. |
| Ví dụ | Để đo độ biến đổi của điểm số của học sinh trong một lớp học. | Để tính sai số của trung bình điểm số mẫu ngẫu nhiên của học sinh từ quần thể toàn trường. |
| Thông tin thường thấy trong | Báo cáo kết quả thống kê, biểu đồ tần số, phân tích phân phối dữ liệu. | Bài báo cáo kết quả thống kê, kiểm định giả thuyết, xây dựng khoảng tin cậy. |
5. Ý nghĩa của Sai số chuẩn độ
Sai số chuẩn độ (Standard Error) là một đại lượng thống kê có ý nghĩa quan trọng trong nghiên cứu thống kê và đánh giá. Nó thể hiện mức độ không chắc chắn trong ước tính tham số của một quần thể dựa trên một mẫu ngẫu nhiên từ quần thể đó. Dưới đây là một số ý nghĩa quan trọng của sai số chuẩn độ:
- Đo lường không chắc chắn: Sai số chuẩn độ đo lường mức độ không chắc chắn trong việc ước tính tham số (ví dụ: trung bình, tỷ lệ) của quần thể dựa trên mẫu ngẫu nhiên. Nó cho biết mức độ biến đổi mà bạn có thể mong đợi khi bạn lấy mẫu ngẫu nhiên khác từ cùng một quần thể.
- Xây dựng khoảng tin cậy: Sai số chuẩn độ được sử dụng để tính toán khoảng tin cậy cho ước tính tham số. Khoảng tin cậy giúp xác định mức độ tin cậy của ước tính và cho phép bạn biết đến khoảng giá trị mà tham số thực sự nằm trong đó với một xác suất nhất định.
- Kiểm định giả thuyết: Trong các phân tích thống kê, sai số chuẩn độ được sử dụng để tính toán giá trị t- và kiểm tra giả thuyết thống kê. Nó cho phép bạn đánh giá xem liệu sự khác biệt giữa các mẫu có ý nghĩa thống kê hay không.
- So sánh kết quả: Sai số chuẩn độ cung cấp thông tin quan trọng để so sánh các kết quả thống kê giữa các nhóm hoặc điều kiện khác nhau. Nó giúp đảm bảo rằng bất kỳ sự khác biệt nào giữa các nhóm là ý nghĩa thống kê.
- Quyết định nên tiếp tục hay ngừng thu thập dữ liệu: Khi nghiên cứu hoặc khảo sát đang được tiến hành, sai số chuẩn độ có thể giúp đánh giá xem liệu mẫu ngẫu nhiên đã đủ lớn để đạt được sự biểu đạt thống kê đáng tin cậy, hoặc liệu bạn cần tiếp tục thu thập dữ liệu thêm.
6. Ứng dụng của Sai số chuẩn độ trong các lĩnh vực
Sai số chuẩn độ (Standard Error, SE) có ứng dụng trong nhiều lĩnh vực và ngành khác nhau. Dưới đây là một số ví dụ về cách nó được sử dụng trong các ngành chính:
Y tế và Y học lâm sàng:
- Trong nghiên cứu lâm sàng, sai số chuẩn độ thường xuất hiện khi đánh giá hiệu quả của một liệu pháp hoặc thuốc.
- Nó được sử dụng để tính khoảng tin cậy cho giá trị trung bình của chỉ số sức khỏe trong một quần thể.
Tài chính và kinh tế:
- Trong phân tích tài chính, sai số chuẩn độ có thể được sử dụng để đo lường mức độ không chắc chắn trong việc ước tính giá trị tài sản hoặc thị trường.
- Trong mô hình hồi quy tài chính, nó có thể đánh giá độ chính xác của dự đoán thị trường tài sản.
Giáo dục:
- Trong giáo dục, sai số chuẩn độ có thể được sử dụng để đo lường mức độ không chắc chắn trong ước tính thành tích học tập của học sinh.
- Nó có thể giúp đánh giá sự khác biệt trong hiệu suất giữa các lớp học hoặc trường học.
Nghiên cứu xã hội và hành vi con người:
- Trong nghiên cứu xã hội, sai số chuẩn độ có thể được sử dụng để đo lường độ biến đổi của biến thích nghiên cứu trong mẫu ngẫu nhiên.
- Nó cũng có thể giúp xác định mức độ không chắc chắn khi bạn so sánh các nhóm dân số.
Nông nghiệp và môi trường:
- Trong lĩnh vực nông nghiệp, sai số chuẩn độ có thể được sử dụng để đo lường độ biến đổi trong sản lượng nông sản dựa trên dữ liệu từ các mẫu ngẫu nhiên.
- Trong môi trường, nó có thể đánh giá độ chính xác của ước tính số lượng và loại loài trong một khu vực.
Quản lý dự án và kỹ thuật:
- Trong quản lý dự án, sai số chuẩn độ có thể được sử dụng để đo lường mức độ không chắc chắn trong việc dự đoán thời gian và nguồn lực cần thiết cho dự án.
- Trong kỹ thuật, nó có thể giúp đánh giá độ chính xác của kết quả và đảm bảo sự ổn định trong quy trình sản xuất hoặc dịch vụ.
Như vậy, sai số chuẩn độ có ứng dụng đa dạng trong nhiều lĩnh vực khác nhau và giúp cải thiện độ chính xác và tin cậy trong việc đánh giá và đưa ra quyết định dựa trên dữ liệu thống kê.
Xem thêm: Sai Số Chuẩn Là Gì? Ý Nghĩa, Công Thức Và Ứng Dụng
Bài viết đã trình bày một cái nhìn tổng quan chi tiết và cụ thể về Sai số chuẩn độ, bao gồm cả khái niệm, công thức, ý nghĩa và ứng dụng của nó. Hy vọng rằng nội dung này sẽ là một nguồn thông tin hữu ích để nâng cao kiến thức thống kê của bạn. Chúc bạn thành công trong việc áp dụng kiến thức này vào thực tế!
CEO Helen Lưu Hà Chi – Nhà sáng lập website luanvanviet.com , nơi cung cấp các dịch vụ viết thuê luận văn thạc sĩ, tốt nghiệp, tiểu luận, essay, Assignment, cùng với các giải pháp chuyên sâu về xử lý số liệu bao gồm SPSS, STATA, EVIEWS, và SmartPLS.
