Phân tích hồi quy tuyến tính là một kỹ thuật thống kê được sử dụng phổ biến trong các công trình nghiên cứu khoa học. Đặc biệt, để tạo ra một bài làm chất lượng, đòi hỏi người thực hiện phải phân tích các biến này trong SPSS. Cùng tìm hiểu các bước để phân tích hồi quy tuyến tính trong SPSS trong bài viết dưới đây nhé!
- 1. Định nghĩa về Phân tích hồi quy tuyến tính
- 2. Phương trình hồi quy tuyến tính
- 3. 4 giả định trong hồi quy đa biến
-
4. Phân tích hồi quy tuyến tính trong SPSS
- 4.1. Phân tích hồi quy tuyến tính đơn giản
- Bước 1. Nhập dữ liệu vào từng ô tương ứng
- Bước 2. Vào Menu -> Analyze -> Regression -> Linear
- Bước 3. Sau khi chạy xong, ta có thể đọc được các kết quả trên màn hình
- Bước 4. Sau khi xác định xong các đại lượng, lập được phương trình đường thẳng hồi quy thì tiến hành vẽ đường thẳng hồi quy trong SPSS
- 4.2. Phân tích hồi quy tuyến tính bội
- Bước 1. Vào Analyze -> Regression -> Linear
- Bước 2. Đưa các biến phụ thuộc vào ô Dependent, các biến độc lập vào ô Independents tương ứng.
- Bước 3. Chọn Statistics -> Continue
- Bước 4. Vào Plots -> Tích chọn Histogram và Normal Probability Plot, kéo biến ZRESID vào ô y và biến ZPRED vào ô X -> Continue
- Bước 5. Quay lại giao diện ban đầu, chọn Method tương ứng -> Chọn Enter hoặc Stepwise -> Ok
- Bước 6. Hoàn thành và đọc kết quả
1. Định nghĩa về Phân tích hồi quy tuyến tính
Định nghĩa chung
- Phân tích hồi quy tuyến tính là phương pháp phân tích mối quan hệ giữa biến phụ thuộc Y với một hoặc nhiều biến độc lập X. Mô hình sử dụng hàm tuyến tính (bậc 1). Các tham số (hoặc hàm số) của mô hình được ước tính từ dữ liệu.
- Hồi quy tuyến tính được sử dụng rộng rãi trong thực tế do tính chất đơn giản hóa của nó. Nó cũng dễ dàng để ước tính.
Khi tiến hành kiểm định các giả thuyết về mối quan hệ giữa hai hay nhiều biến, bao gồm một biến phụ thuộc hay nhiều biến độc lập:
- Nếu chỉ có một biến độc lập, mô hình được gọi là hồi quy tuyến tính đơn biến SLR (Simple Linear Regression)
- Nếu có hai hoặc nhiều biến độc lập, mô hình được gọi là hồi quy đa biến trong spss MLR (Multiple Linear Regression).
2. Phương trình hồi quy tuyến tính
2.1. Phương trình hồi quy tuyến tính đơn
Y = β0 + β1X + e
Trong đó:
- Y: Biến phụ thuộc.
- X: Biến độc lập.
- β0: Hằng số hồi quy.
- β: Hệ số hồi quy.
- e: Sai số.
Trường hợp có thể sử dụng
Bạn có thể sử dụng mô hình hồi quy đơn để lập mô hình mối quan hệ giữa hai biến đơn giản, ví dụ như:
- Lượng mưa và sản lượng trồng cây ăn quả.
- Độ tuổi và chiều cao của trẻ em.
- Nhiệt độ và sự gia tăng mực nước biển.
2.2. Phương trình hồi quy tuyến tính bội
Y = β0 + β1X1 + β2X2 + … + βnXn + e
Trong đó:
- Y: Biến phụ thuộc.
- X, X1, X2, Xn: Biến độc lập.
- β0: Hằng số hồi quy.
- β1, β2, βn: Hệ số hồi quy.
- e: Sai số.
Trường hợp có thể sử dụng
Bạn có thể sử dụng mô hình hồi quy đơn để lập mô hình mối quan hệ giữa các biến phức tạp hơn, như:
- Lượng mưa, nhiệt độ và tần suất sử dụng phân bón đối với cây ăn quả.
- Chế độ ăn uống và cường độ tập luyện đối với bệnh nhân tim mạch.
- Lạm phát và việc điều chỉnh mức tiền lương cho nhân viên làm việc lâu năm.
3. 4 giả định trong hồi quy đa biến
3.1. Mối quan hệ tuyến tính
Mối quan hệ tuyến tính tồn tại giữa các biến độc lập và phụ thuộc. Theo đó, người thực hiện phải tạo ra một biểu đồ phân tán ngẫu nhiên các giá trị x – y để xem liệu chúng có nằm trên một đường thẳng hay không. Hoặc, có thể áp dụng các hàm phi tuyến tính để tạo ra mối quan hệ tuyến tính giữa hai biến về mặt toán học.
3.2. Phần dư độc lập
Người nghiên cứu dữ liệu sử dụng phần dư để đo lường độ chính xác của các dự đoán. Phần dư là sự khác biệt giữa dữ liệu được quan sát và giá trị dự đoán. Các dư lượng không được có bất kỳ mô hình nhận dạng nào giữa chúng.
3.3. Tính chuẩn
Các kỹ thuật vẽ đồ thị như biểu đồ Q-Q xác định xem phần dư có phân phối chuẩn hay không. Phần dư nằm dọc theo một đường chéo ở giữa đồ thị. Loại bỏ các giá trị ngoại lai hoặc thực hiện chuyển đổi phi tuyến tính có thể khắc phục sự cố.
3.4. Phương sai không đổi
Phương sai không đổi giả định rằng phần dư có phương sai cố định hoặc một độ lệch chuẩn so với giá trị trung bình đối với tất cả các giá trị của x. Nếu không, kết quả quét có thể không chính xác. Nếu giả định này không được thỏa mãn, bạn có thể cần sửa đổi biến phụ thuộc.
4. Phân tích hồi quy tuyến tính trong SPSS
4.1. Phân tích hồi quy tuyến tính đơn giản
Bước 1. Nhập dữ liệu vào từng ô tương ứng
Bước 2. Vào Menu -> Analyze -> Regression -> Linear
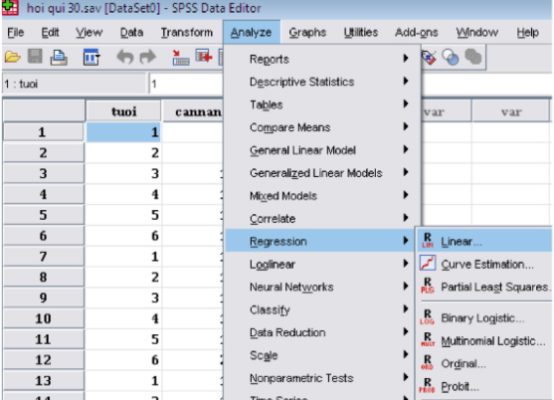
Bước 3. Sau khi chạy xong, ta có thể đọc được các kết quả trên màn hình
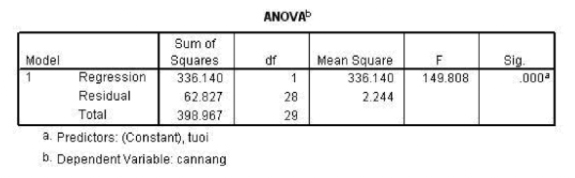
Bước 4. Sau khi xác định xong các đại lượng, lập được phương trình đường thẳng hồi quy thì tiến hành vẽ đường thẳng hồi quy trong SPSS
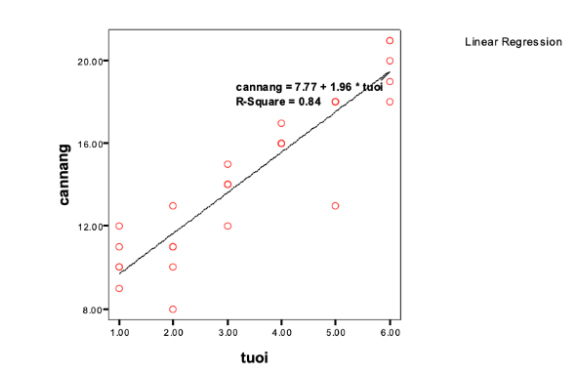
4.2. Phân tích hồi quy tuyến tính bội
Bước 1. Vào Analyze -> Regression -> Linear
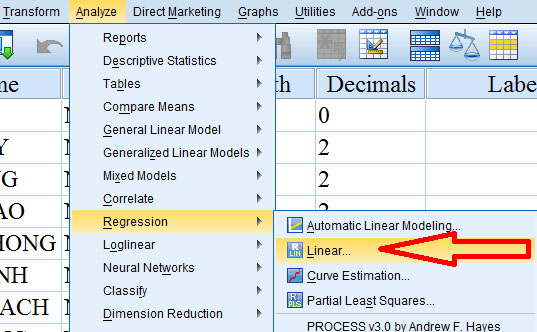
Bước 2. Đưa các biến phụ thuộc vào ô Dependent, các biến độc lập vào ô Independents tương ứng.
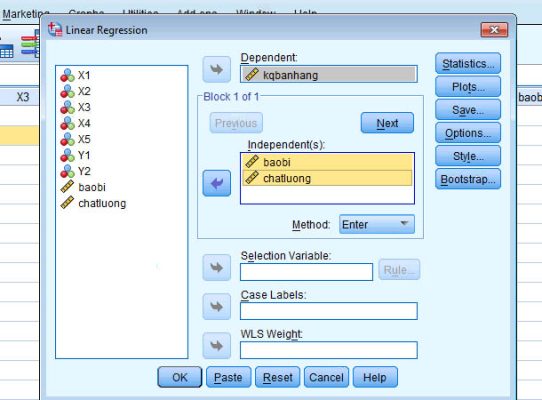
Bước 3. Chọn Statistics -> Continue
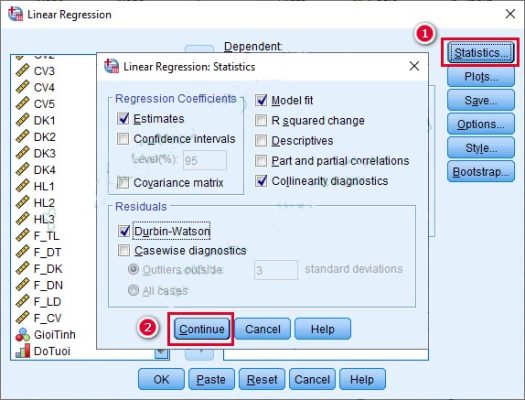
Bước 4. Vào Plots -> Tích chọn Histogram và Normal Probability Plot, kéo biến ZRESID vào ô y và biến ZPRED vào ô X -> Continue
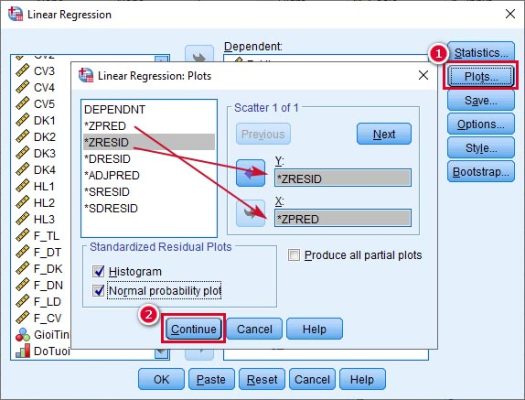
Bước 5. Quay lại giao diện ban đầu, chọn Method tương ứng -> Chọn Enter hoặc Stepwise -> Ok
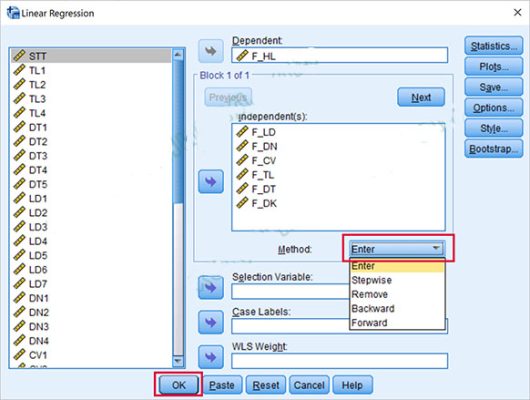
Bước 6. Hoàn thành và đọc kết quả
Trên đây là một vài thông tin cơ bản nhất về phân tích hồi quy tuyến tính trong SPSS. Hy vọng bài viết của chúng tôi sẽ giúp ích được cho bạn. Nếu có bất kỳ vấn đề gì, vui lòng liên hệ với Luận Văn Việt để được tư vấn sớm nhất!
Hiện tại tôi đang đảm nhiệm vị trí Content Leader tại Luận Văn Việt. Tất cả các nội dung đăng tải trên website của Luận Văn Việt đều được tôi kiểm duyệt và lên kế hoạch nội dung. Tôi rất yêu thích việc viết lách ngay từ khi còn ngồi trên ghế nhà trường. Và đến nay thì tôi đã có hơn 5 năm kinh nghiệm viết bài.
Hy vọng có thể mang đến cho bạn đọc thật nhiều thông tin bổ ích về tất cả các chuyên ngành, giúp bạn hoàn thành bài luận văn của mình một cách tốt nhất!
