Kiểm Định Trung Bình Tổng Thể: Khái Niệm, Phân Loại, Cách Thực Hiện 2024

Kiểm định trung bình tổng thể được sử dụng vô cùng phổ biến, trong việc đưa ra phân tích, lập luận về một nhận định nào đó. Tuy nhiên, phương pháp này sẽ rất dễ gây nhầm lẫn trong quá trình sử dụng. Hiểu được điều này, Luận Văn Việt xin bật mí đến bạn đọc những kiến thức cơ bản liên quan đến kiểm định trung bình tổng thể. Mời các bạn cùng đón đọc!

1. Kiểm định trung bình tổng thể (Independent Samples T-Test)

Kiểm định trung bình tổng thể là phương pháp được dùng để so sánh, phân tích giá trị trung bình của quần thể này với giá trị trung bình trong giả thiết hoặc đơn giản là với giá trị trung bình của quần thể khác. Từ đó, các nhà nghiên cứu có thể áp dụng phương pháp này để kiểm định số liệu, và đưa ra những lập luận, nhận định mang đến kết quả chính xác nhất.

1.1. Trường hợp sử dụng

Một số trường hợp có thể sử dụng phương pháp kiểm định trung bình tổng thể như: 

• Kiểm tra trung bình điểm tiếng anh của học sinh nữ, nam lớp 9A có sự khác nhau hay không, nhóm nào học tốt hơn?
• Kiểm tra trung bình tỷ lệ sinh trưởng của cây ngô và cây lạc trong cùng một thửa đất có khác nhau hay không, trung bình tỷ lệ sinh trưởng của cây ngô hay cây lạc cao hơn?

1.2. 4 bước thực hiện chính 

• Bước 1: Chọn Analyze > Compare Means > Independent-Samples T Test.
• Bước 2: Di chuyển biến độc lập vào ô Grouping Variable field và chuyển biến cần kiểm định (biến phụ thuộc) vào ô Test Variable(s). 
• Bước 3: Nhấp vào Define Groups để mở ra một cửa sổ mới. Sử dụng các giá trị được chỉ định được chọn theo mặc định. Nhấp vào Continue khi hoàn tất.
• Bước 4: Nhấp vào OK để chạy Independent-Samples T Test. Đầu ra cho phân tích sẽ hiển thị trong cửa sổ Output Viewer.

1.3. Ví dụ cụ thể

Đề bài:  Nhà nghiên cứu đã tuyển chọn ngẫu nhiên một mẫu nam giới không hoạt động được phân loại là thừa cân. 

Mẫu này sau đó được chia ngẫu nhiên thành hai nhóm: 

• Nhóm 1 trải qua chế độ ăn kiêng kiểm soát lượng calo 
• Nhóm 2 thực hiện chương trình tập luyện. 

Yêu cầu: Xác định chương trình điều trị (biến Treatment) nào hiệu quả hơn, nồng độ cholesterol (biến Cholesterol) trung bình được so sánh giữa hai nhóm khi kết thúc chương trình điều trị.

Cách thực hiện:

Bước 1: Mở SPSS, chọn Analyze > Compare Means > Independent-Samples T Test.

Bước 2: Di chuyển biến Treatment vào ô Grouping Variable field và chuyển biến Cholesterol vào ô Test Variable(s). 

Bước 3: Nhấp vào Define Groups để mở ra một cửa sổ mới. Nhập “1” vào ô Group 1 và nhập  “2” vào ô Group 2. Nhấp vào Continue khi hoàn tất. 

Bước 4: Nhấp vào OK để chạy Independent-Samples T Test. Đầu ra cho phân tích sẽ hiển thị trong cửa sổ Output Viewer.

Bảng Output

Bảng thống kê nhóm (Group Statistics)

Bảng Independent Samples Test

Báo cáo kết quả : Nghiên cứu này cho thấy những người nam bị thừa cân Nhóm 1 có nồng độ cholesterol thấp hơn đáng kể (5,80 ± 0,38 mmol/L) so với Nhóm 2 (6,15 ± 0,52 mmol/L), t (38)=2,428, p = 0,020.

2. Kiểm định trung bình một tổng thể (One-Sample T-Test)

Kiểm định trung bình của một tổng thể – One sample T-Test được coi là phương pháp kiểm định phổ biến, được sử dụng nhiều trên phần mềm SPSS.

2.1. Trường hợp sử dụng

 Phương pháp này được sử dụng trong các trường hợp cần phân tích mối liên quan giữa giá trị trung bình của tổng thể đó với một giá trị được xác định cụ thể từ trước.

2.2. 3 bước thực hiện chính

• Bước 1: Chọn Analyze trên thanh công cụ > Compare Means > One Sample T Test.
• Bước 2: Trong cửa sổ One- Sample T Test, bạn chuyển biến cần kiểm định vào ô Test Variable(s).
• Bước 3: Chọn Option > nhập độ tin cậy > Continue > Ok, sau đó nhận kết quả. Lúc này, bảng One- Sample Statistic hiện ra, cho ta biết trung bình biến và độ lệch chuẩn của biến.

2.3. Ví dụ cụ thể

Đề bài: Một nhà nghiên cứu đã tuyển 40 người tham gia vào một nghiên cứu can thiệp tâm lý, mô tả mức độ trầm cảm.

• Điểm trầm cảm được ghi lại trong biến dep_score.
• Yêu cầu: Nhà nghiên cứu muốn biết liệu mẫu của ông có đại diện cho dân số bình thường hay không (tức là họ có điểm số khác biệt đáng kể về mặt thống kê so với 4,0).

Cách thực hiện:

Bước 1: Chọn Analyze trên thanh công cụ > Compare Means > One Sample T Test.

Bước 2: Trong cửa sổ One- Sample T Test, bạn chuyển biến dep_score. cần kiểm định vào ô Test Variable(s).

Bước 3: Chọn Option > nhập độ tin cậy > Continue > Ok, sau đó nhận kết quả. Lúc này, bảng One- Sample Statistic hiện ra, cho ta biết trung bình biến và độ lệch chuẩn của biến.

Bảng Output

Bảng Descriptive statistics

Bảng One-sample t-test

Bảng Standardised effect sizes

Báo cáo kết quả:

• Điểm trầm cảm trung bình (3,72 ± 0,74) thấp hơn điểm trầm cảm “bình thường” của dân số là 4,0.
• Điểm trầm cảm thấp hơn đáng kể về mặt thống kê so với điểm trầm cảm bình thường của dân số, t (39) = -2,381, p = 0,022.
• Điểm trầm cảm thường có phân phối bình thường, được đánh giá bằng thử nghiệm của Shapiro-Wilk ( p > 0,05) và không có ngoại lệ nào trong dữ liệu, được đánh giá bằng cách kiểm tra biểu đồ hộp. 
• Điểm trầm cảm trung bình (3,73 ± 0,74) thấp hơn điểm trầm cảm bình thường là 4,0. Chênh lệch có ý nghĩa thống kê là 0,28 (KTC 95%, 0,04 đến 0,51), t (39) = -2,381, p = 0,022.

3. Kiểm định hai trung bình

Kiểm định hai trung bình là một phương pháp thống kê được sử dụng để xác định xem có sự khác biệt ý nghĩa giữa hai giá trị trung bình của hai nhóm dữ liệu khác nhau hay không?

3.1. Trường hợp sử dụng

• Phương pháp này nhằm dựa trên hai mẫu độc lập được rút ra từ hai tổng thể, để từ đó kiểm định giả thuyết về sự bằng nhau của hai trung bình tổng thể đó.
• Ngoài ra, để tính trung bình ta có thể dùng một biến định lượng, để chia nhóm so sánh ta có thể dùng một biến định tính trong những trường hợp kiểm định sai khác trung bình.

3.2. 3 bước thực hiện

• Bước 1: Trên thanh công cụ chọn Analyze > Compare Means > Independent – Sample T Test.
• Bước 2: Trong cửa sổ mới, chuyển biến 1 vào Test Variable(s), biến 2 vào ô Grouping Variable > điều chỉnh độ tin cậy trong Options.
• Bước 3: Chọn Define Groups > Nhập giá trị group 1 và 2 theo yêu cầu > Continue. Bảng kết quả hiển thị cho thấy giá trị cho cả hai trường hợp là tổng thể bằng nhau và không bằng nhau.

3.3. Ví dụ cụ thể

Đề bài: Các nhà nghiên cứu muốn biết liệu phương pháp xử lý nhiên liệu mới có dẫn đến sự thay đổi số dặm trung bình trên mỗi gallon của một chiếc ô tô nào đó hay không?

• Nhà nghiên cứu tiến hành một thí nghiệm trong đó 12 ô tô được xử lý nhiên liệu mới còn 12 ô tô thì không.
• Chỉ số mpg của từng ô tô cùng với nhóm chúng thuộc về (0 = không xử lý nhiên liệu, 1 = xử lý nhiên liệu):

Cách thực hiện:

Bước 1: Trên thanh công cụ chọn Analyze > Compare Means > Independent – Sample T Test.

Bước 2: Trong cửa sổ mới, chuyển biến mmg vào Test Variable(s), biến group vào ô Grouping Variable > điều chỉnh độ tin cậy trong Options.

Bước 3: Chọn Define Groups > Nhập giá trị group 1 và group 2 theo yêu cầu > Continue để hiển thị kết quả đầu ra Output.

Bảng Output

Bảng đầu tiên hiển thị số liệu thống kê tóm tắt sau cho cả hai nhóm: 

• N
• Mean
• Std. Deviation
• Std. Error Mean

Bảng thứ hai hiển thị kết quả của hai mẫu t-test:

• Hàng đầu tiên hiển thị kết quả kiểm tra nếu bạn giả định rằng phương sai giữa hai nhóm là bằng nhau. 
• Hàng thứ hai hiển thị kết quả kiểm tra nếu bạn không đưa ra giả định này.

Báo cáo kết quả

Trong trường hợp này, hai phiên bản thử nghiệm đều cho kết quả gần như giống nhau. Vì vậy, chúng ta sẽ chỉ tham khảo kết quả của hàng đầu tiên bảng thứ 2:

• t:  Thống kê kiểm tra, được tìm thấy là -1,428
• df:  Bậc tự do, được tính bằng n 1 +n 2 -2 = 12+12-2 = 22
• Sig. (2-tailed):  Giá trị p hai mặt tương ứng tại giá trị -1,428 với df=22
• Mean Difference:  Sự khác biệt giữa hai phương tiện mẫu
• Std. Error Difference:  Sai số chuẩn của chênh lệch trung bình
• 95% C.I. of the Difference:  Khoảng tin cậy 95% cho sự khác biệt thực sự giữa hai trung bình tổng thể.

Vì giá trị p-value = 0.167) > 0.05 nên không thể bác bỏ giả thuyết khống. Do đó, không có đủ bằng chứng để nói rằng mpg trung bình thực sự là khác nhau giữa những chiếc xe được xử lý và những chiếc xe không được xử lý.

4. Kiểm định trung bình cho cặp 

Kiểm định trung bình cho cặp là phương pháp có những ưu điểm vượt trội, được sử dụng khi thực hiện kiểm định giả thiết thông qua phần mềm SPSS. Kiểm định trung bình cho cặp giúp loại trừ các nhân tố ảnh hưởng từ bên ngoài, tác động vào nhóm thử. Vì thế, người ta thường dùng phương pháp này với dạng thử nghiệm trước và sau.

4.1. Trường hợp sử dụng

Trong trường hợp hai mẫu phải có sự tương đồng về kích cỡ, cũng như sự chênh lệch giữa các giá trị trong hai mẫu đảm bảo có phân phối chuẩn.

4.2. Các bước thực hiện

• Bước 1: Chọn Analyze > Compare Means > Paired- Sample T Test.
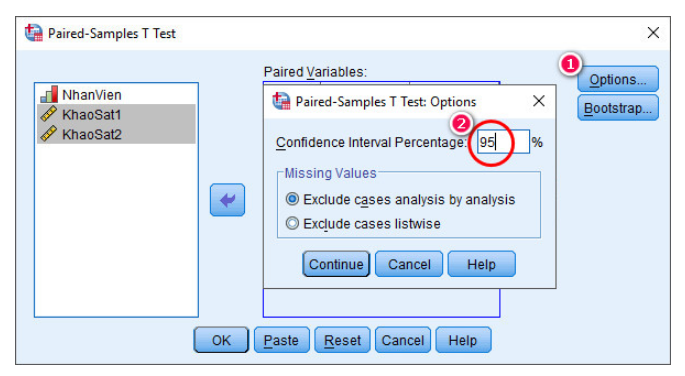
• Bước 2: Ô cửa sổ của Paired- Sample T Test, bạn đưa biến lần lượt vào ô Variable 1, và Variable 2 > chỉnh độ tin cậy trong Options.
• Bước 3: Chọn OK để xem kết quả. 

4.3. Ví dụ cụ thể

Đề bài: Một nhóm sinh viên Khoa học Thể thao ( n = 20) được chọn để điều tra xem liệu chương trình huấn luyện plyometric kéo dài 12 tuần có cải thiện thành tích nhảy xa đứng của họ hay không?

• Biến phụ thuộc là “standing long jump performance – thành tích nhảy xa đứng”, và hai nhóm liên quan là giá trị đứng nhảy xa “before – trước” và “after – sau” chương trình đào tạo plyometric 12 tuần.

Cách thực hiện:

Bước 1: Chọn Analyze > Compare Means > Paired- Sample T Test.

Bước 2: Ô cửa sổ của Paired- Sample T Test, bạn đưa lần lượt biến before và after vào ô Variable 1, và Variable 2 .

Bước 3: Chỉnh độ tin cậy trong Options > Chọn OK để xem kết quả. 

Bảng Output

Bảng Paired Sample Statistics

Bảng Paired Sample Test

Báo cáo kết quả:

• Gía trị t (19) = -4,773, p < 0,0005. 
• Do phương tiện của hai lần nhảy và hướng của giá trị t, chúng ta có thể kết luận rằng có sự cải thiện đáng kể về mặt thống kê về khoảng cách nhảy sau chương trình huấn luyện plyometric từ 2,48 ± 0,16 m lên 2,52 ± 0,16 m ( p < 0,0005 ); cải thiện 0,03 ± 0,03 m.

Hy vọng những chia sẻ trên của Luận Văn Việt đã giúp bạn hiểu phần nào về kiểm định trung bình tổng thể, góp phần hỗ trợ bạn trong quá trình nghiên cứu, phân tích của mình. Bạn đọc có thể tìm kiếm những tài liệu bổ ích khác trên website của Luận Văn Việt. Ngoài ra, hãy liên hệ với chúng tôi qua số số điện thoại 0915 686 999 hoặc email luanvanviet.group@gmail.com để được giải đáp thắc mắc và tư vấn các gói dịch vụ một cách chi tiết. Cảm ơn các bạn đã đón đọc!

Lưu Hà Chi( Content Leader )

CEO Helen Lưu Hà Chi – Nhà sáng lập website luanvanviet.com , nơi cung cấp các dịch vụ viết thuê luận văn thạc sĩ, tốt nghiệp, tiểu luận, essay, Assignment, cùng với các giải pháp chuyên sâu về xử lý số liệu bao gồm SPSS, STATA, EVIEWS, và SmartPLS.